Complexity Forum science page

Komplexitet
Studier av ekologiska och sociala system, teoretisk fysik (icke-jämviktsystem) och framför allt datorsimuleringar, har under senare år givit oerhört intressanta resultat som ännu inte nått den stora allmänheten eller spridit sig till angränsande vetenskaper.
Lite löst talar man om komplexitetsteori som sammanfattande beteckning för samband som man finner i vitt skilda samanhang. Somliga teoretiska fysiker kallar det något som ligger bakom fysiken. Komplexitetsteori är inte metafysik, men ändå mer fundamentalt än fysiken själv.
För tydlighets skull skiljer vi på komplicerad och komplex.
Med hjälp av simuleringar och genom studier av naturen har man gjort en mängd iakttagelser av typen.

Ett komplext system, som drivits till kritiskt tillstånd, edge of chaos, har sin egen högsta beräkningshastighet. Det innebär att systemet inte kan simuleras med tillräcklig noggrannhet snabbare än systemet självt utvecklas. Ett sådant system kan vara helt deterministiskt, men ändå fullständigt opredikterbart.
Till grund för ett komplext system kan ligga ett fåtal enkla regler.
Komplexa system uppvisar ofta nätverksstruktur.
Komplexa system kan uppvisa "emergence", som är oväntade, ofta oförutsebara egenskaper hos systemet som är ett resultat av interaktionen mellan systemets element.
Komplexa system kan ha en adaptiv förmåga att påverka sin miljö och till och med sig själv. Sådana system kallas CAS, complex adaptive systems.
Komplexa system kan vara ickepredikterbara på ett plan, men slående regelbundna på ett annat (väder gentemot klimat).
Försök att styra ett komplext system kan ge oväntade resultat.
Komplexa system kan ofta beskrivas med potensfunktioner (de är skalningsfria).

Jordbävningar. Om man plottar jordbävningars energi (Richterskalan) mot antal jordbävningar så fås en rät linje i ett log-log diagram.
        När kontinentalplattorna glider mot varandra så skapar spänningar i berggrunden små brott varje sekund. Ibland samverkar flera brott och då blir störningen lite större. Någon gång kan det uppstå ett närverk av zoner i berget som befinner sig nära bristningsgränsen och då kan ett litet brott någonstans genom att föra över lasten på omkringliggande delar ge upphov till en lavin av brott som vi uppfattar som en jordbävning.
        Små sprickor, som är för små för att vi skall märka dem, och jordbävningar som krossar städer och dödar hundratusentals människor har exakt samma orsaker. De tillhör samma potensfunktion. När den första sprickan bildas finns ingen möjlighet att förutsäga hur stor den kommer att bli. Det finns ingen typisk storlek och storleken på nästa skalv kan inte förutsägas.
        Vi är inte vana vid att det är så. Vi har lärt oss att det mesta är normalfördelat, att Gausskurvan beskriver världen, och visst, den fungerar fint i många samanhang. Om vi tex mäter längden på människor eller vikten på potatisar och plottar denna mot antal så får vi den välkända klockformade Gausskurvan. Dessa variabler är normalfördelade och det finns en typisk storlek. Några få är mycket mindre eller mycket större, men de flesta mitt emellan.

Potatiskross. Om vi nu djupfryser potatisarna vi vägde i förra exemplet och därefter kastar dem i väggen så att de krossas i bitar och plockar upp bitarna, väger dessa och antecknar hur många det blir av olika storlek så finner vi en potensfuntion, en rät linje i log-log diagrammet när vi plottar vikt mot antal.

Man finner potensfunktioner för

Antal krig - antal dödade i kriget
Börskursändringars storlek - antal ändringar av varje storlek
Antal individer av varje art i en biotop - vikten på en individ av varje art
Storleken på städer - antal av varje storlek
Skogsbränders storlek - antal av varje storlek
Antal hjärtslag - puls (mätte på mig själv under 13 h 43 min, se ovanstående fig !)
Antal länkar som pekar på en webbplats - antal webbplatser av varje storlek

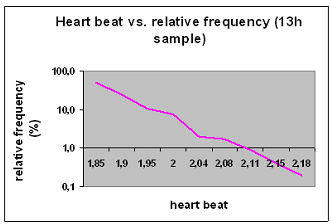
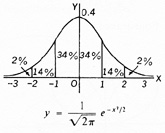
Bakom många fenomen i de mest skilda samanhang döljer sig alltså potensfunktionen som har följande speciellt fantasieggande egenskaper.
- Det finns ingen typisk storlek, processen är skalningsfri (scale free).
- Likartade händelser av alla storlekar är lika naturliga och har i grunden samma orsaker om de tillhör samma potensfunktion (samma exponent).
- Man kan aldrig avgöra om en händelse styrd av en potensfunktion kommer att bli stor, liten, eller mittemellan.
- Processerna har sin grund i:

Ett slags geometriskt förhållande mellan elementen. Hur elementen påverkar varandra över avstånd har betydelse. Ibland påverkar ett element många andra element och ibland bara några få. Elementen är delar av ett nätverk med kopplingar av varierande styrka.
Den fortsatta utvecklingen från där vi befinner oss beror av den väg vi kom hit. Historien ligger inbakad i samtiden och kan fungera som triggningspunkter för ofta otänkbara händelseförlopp.
Systemet driver sig själv till kritikalitet, edge of chaos, tex så utnyttjar allt levande sin biotop till bristningsgränsen. I naturen finns ingen måttfullhet eller framförhållning varför det ofta uppstår kriser. Oftast dör bara en art ut åt gången, men ibland vart 200-miljonte år eller så brakar globala ekosystem samman och vi får massutrotning av arter av precis samma orsaker som när bara någon eller några få dör ut.

Stora händelser måste ha stora orsaker, så vill vi gärna tänka, men som framgått av det ovanstående kan de största händelser ha de minsta orsaker.

En ny strategi
Konsekvensen av de vetenskapliga resultaten är att man inte kan vara så säker, som man tidigare trott, att framtiden kan predikteras. Exempelvis är den teoretiska gränsen för en väderprognos tre veckor och kommer aldrig att kunna överträffas.
Mycket stora och mycket små händelser kan ha samma orsak och man kan inte när händelsen faller ut säga om den kommer att bli betydelsefull eller inte. Möjligheten att förutse framtiden är liten och oväntade saker kan hända plötsligt. Självklart har allt detta en avgörande betydelse för vårt val av strategi.
Planer kommer inte att hålla, men planering av olika alternativ blir viktigare och flexibiliteten och beredskapen måste öka liksom förmågan att se vad som håller på att hända. Vi belyser detta med utgångspunkt i Boyds strategimodell, OODA-loopen (efter Col. USAF John R. Boyd, 1900-talets kanske störste strateg).

Observation - utan filter eller skygglappar. Observera med ett fritt och flytande sinne. Fastna inte vid något objekt.
Orientering - destruktion & skapande, kasta gammal bråte överbord, skapa nya mentala modeller.
Decision - ibland måste besluten komma tveklöst. (Stora beslut fattas inom sju hjärtslag. Små beslut får ta längre tid. - Hagakure av Yamamoto Tsunetomo).
Act - flexibelt smidigt genomförande av besluten.

Munenori & Takuan (Munenori: minister & fäktlärare till Japans shogun och Munenori: zen-buddistisk abbot och ledande intellektuell, båda under 1600-talets första hälft) talar om principer och förhållningssätt som stöder och harmonierar med OODA-loopens delar. I klassisk Budo finns komponenter som är användbara, belysande, och klargörande.
        Förmågan till förändring är fundamental liksom förmågan till organisering. Det gäller att snabbt organisera från inget eller från en icke ändamålsenlig organisation till en som är väl anpassad till de nya omständigheterna. Detta måste kunna ske, så att säga ur marschgruppering och dessutom inte som en regelmässig övning utan plötsligt.
        Det handlar om att öka beredskapen och förmågan att hantera det man aldrig tidigare stött på och att agera och organisera in i en värld man ännu inte känner, att orientera utan karta i ett främmande land.
        Man måste därför driva organisationen till "the edge of chaos eftersom system som befinner sig där har sin egen högsta beräkningskapacitet och anpassar sig till nya omständigheter snabbare än varje annan organisation.

För en fylligare behandling av komplexitet se länktipsen under Links